정렬하기와 자료구조에 대한 블로깅은 ZeroCho님의 블로그 포스트에서 많은 도움을 얻었습니다. 감사합니다.
나무를 뒤집은 모양의 자료구조, 트리(Tree)
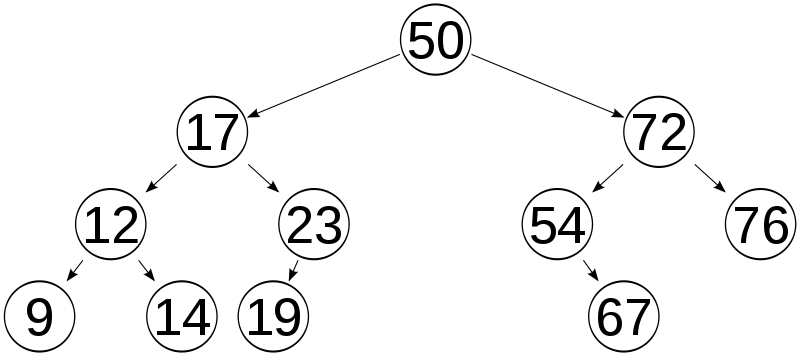
- 루트 노드(최상위 조상 노드)에서 아래로 계속 자식 노드들을 생성하면 뻗는 나무 모양의 자료구조.
- branch, edge : 노드 사이의 연결성을 나타내는 것
- path : 부모 노드에서 자식 노드까지 찾아가는 길, 그리고 그 사이의 edge 개수를 height 라고 부른다.
- leaf : 더 이상 자식 노드를 가지고 있지 않은 노드를 잎 노드라고 할 수 있다.
보통 이진 (탐색, 검색) 트리 구조를 많이 활용한다. 이진 트리는 하나의 부모 노드가 최대 2개의 자식 노드를 가진 트리 구조를 말한다. 그 중에서 이진 탐색 트리는 입력받은 값을 왼쪽, 오른쪽 노드의 값에 비교하면서 입력값 보다 작으면 왼쪽 루트, 크면 오른쪽 루트로 이동하고 반복하여 찾는 구조이다.
class Node (data) {
constructor(data, left, right) {
this.data = data;
this.left;
this.right;
}
}
class Tree {
constructor(count, root) {
this.count = 0;
this.root;
}
}
Tree 클래스를 구성하는 메소드를 만들어야 한다. 우선, 값을 넣고 값이 담긴 노드를 루트나 상위 부모 노드와 연결시켜주는 메소드를 만들자. root에는 새로 생성되는 노드들이 들어가게 된다는 것을 잊지말자.
function compareData(root, node) {
// 최상위 루트가 정해지지 않았으면 해당 루트에 노드를 연결
if (!root) return node;
// 입력받는 노드의 데이터 값과 루트 노드의 데이터 값을 서로 비교
// 작으면 왼쪽으로 다시 보낸다.
if (node.data < root.data) {
root.left = compareData(root.left, node)
return root;
} else {
// 루트보다 크면 오른쪽으로 보낸다.
root.right = compareData(root.right, node);
return root;
}
}
// Tree에 값을 입력하는 메소드 add
add(data) {
let node = new Node(data);
// 구성된 노드가 없으면 새 노드를 루트에 연결
if (this.count === 0) {
this.root = node;
// 이미 만들어진 루트가 있다면, 루트 값과 크기 비교가 필요하다
// 그래서 compareData 함수를 콜백
} else {
compareData(this.root, node);
}
return this.count += 1;
}
다음으로 입력된 값을 찾아주는 메소드를 구성해보자.
- 트리를 구성하고 있는 노드가 있는지, 찾는 데이터가 노드에 값으로 있는지 가장 먼저 파악 > 없다면 false > 재귀의 탈출조건이 된다.
- 찾고자 하는 데이터를 루트에서 부터 비교해가면서 큰지 작은지를 확인한다. 크다면 오른쪽으로 재귀, 작다면 왼쪽으로 재귀하면 된다.
function search(data, node) {
// 찾는 노드가 있는지 없는지
if (node) {
// 있다면, 값과 크기를 비교하여 루트 정하기
// 작다면 왼쪽으로
if (data < node.data) {
return search(data, node.left)
// 크다면 오른쪽으로
} else if (data > node.data) {
return search(data, node.right)
// 바로 원하는 값이 있다면 > 재귀 탈출
} else {
return node;
}
// 찾는 노드가 없거나 처음 구성된 노드가 없다면 > 탈출, false
} else {
return false;
}
}
// 찾는 값의 여부를 알려주는 get 메소드
get(data) {
// root 가 있다면 콜백으로 조회
if (this.root) {
return search(data, this.root);
// 없다면 false!
} else {
return false;
}
}
마지막으로 원하는 값을 트리에서 지워주는 메소드를 작성해야 한다. 가장 구조가 복잡하다. 왜냐하면 제거하면서 이진트리의 구축 요건을 꼭 갖춰야 하기 때문이다.
- 왼쪽 자식 노드가 없는 경우 > 오른쪽 자식을 자기 자리로 끌어올린다.
- 오른쪽 자식 노드가 없는 경우 > 왼쪽 자식 노드를 자리로 끌어올린다.
- 오른쪽, 왼쪽 모두 자식 노드가 있는 경우 > 왼쪽 자식 중에서 가장 큰 값과 자리를 바꾸면 삭제를 하여도 트리 구조 자체의 문제가 발생하지 않는다.
function delete(data, root) {
let newRoot, exchange, temp
// root값이 없다면 false
if (!root) return false;
// 삭제할 데이터가 루트 데이터보다 작다면 왼쪽으로 재귀
if (data < root.data) {
root.left = delete(data, root.left)
// 반대로 크다면 오른쪽으로 재귀
} else if (data > root.data) {
root.right = delete(data, root.right)
// 삭제하고자 했던 노드에 도착했다면
// 이제 이진 트리 구조를 유지하는 경우로 분류
} else {
// 1. 왼쪽 자식이 없다면
if (!root.left) {
newRoot = root.right;
return newRoot;
// 2. 오른쪽 자식이 없다면
} else if (!root.right) {
newRoot = root.left;
return newRoot;
// 3. 오른쪽, 왼쪽 다 자식이 있다면
} else {
// 우선 변경할 값을 임시로 지정
exchange = root.left
// exchange에 지정한 노드 보다 큰 값을 가진 노드가 있다면
// exchange 값을 그 노드의 값으로 변경
// 반복문으로 위치 바꿀 값 결정
while(exchage.right) exchange = exchange.right;
temp = root.data;
root.data = exchange.data;
exchange.data = temp; // -> 이 값을 삭제
root.left = delete(exchange.data, root.left)
}
}
return root;
}
remove(data) {
// 해당하는 데이터를 삭제한 트리 구조를 node에 담았다.
let node = delete(data, this.root)
// 해당하는 데이터가 있다면 root를 노드에 연결
if (node) {
this.root = node;
this.count -= 1;
if(this.count === 0) this.root = null;
}
return true;
}
tree를 이해하는 것은 어려움이 조금 있다. 천천히 자주 반복하여 살펴보고 구조를 이해하는 것에 노력하면 좋을 것 같다.